第二余弦定理は暗記しよう
余弦定理といえば、下記の公式です。
a² =b² + C² - 2bc cosA
三角形のうち、2辺の長さと夾角がわかっている場合に、残りの1辺の長さを求めるときに用います。
しかし実際の試験では、上記の式を変形させた、第二余弦定理を用いることのほうが圧倒的に多いのが実状です。
第二余弦定理を関数電卓で入力しやすいように表示すれば下記のようになります。
cosA = (b² + C² - a²)÷ (2bc)
第二余弦定理は三角形の3辺の長さがわかっていて角度を求める場合に用います。
必要になるたびに余弦定理を変形させていては時間の無駄なので、いつでもすぐに使えるように完璧に覚えましょう。
実際に第二余弦定理を使って角度を算出してみよう!
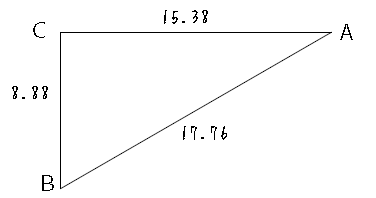
上のように、3辺の長さがわかっている三角形があります。第二余弦定理を用いて∠Aを求めてみましょう。
( 15.38 x² + 17.76 x² - 8.88 x² ) ÷ ( 2 × 15.38 × 17.76 ) =
分子部分も分母部分もカッコでくくりましょう。忘れると数字が異なってきます。正しく入力すると、0.866025404と算出されます。つまり、
cosA = 0.866025404
ということなので、ここから∠Aを算出するにはアークコサインを用います。アークコサインとは、コサインがその数値となるような角度を求める場合に用いるもので、SHIFT cosと入力します。
SHIFT cos =
∠A = 29.99999992が算出されました。
ここで完全に覚えてしまおう!
(第二余弦定理)
cosA = (b² + c² - a²)÷ (2bc)
三角形の3辺の長さがわかっていて角度を求めたい場合に用いる




